Vedic Science helps Mastering Geometric Transformations
Mastering the Geometric Transformations using Vedic Science
In our previous post, we delved into the fundamental geometric shapes—squares, circles, triangles, and rectangles—through the lens of Vedic science. These shapes form the core of both geometry and Vedic practices, symbolizing harmony, balance, and spiritual alignment. We explored how these constructions, rooted in the ancient knowledge of the Sulba Sutras, serve as a strong foundation for understanding both mathematical precision and cosmic order, illustrating how Vedic Science helps mastering geometric transformations.
To deepen our understanding, the Sulba Sutras, written between 800 and 500 BCE, stand as some of the earliest systematic expositions on geometry. Not merely theoretical, these texts were integral to constructing Vedic altars, requiring precise measurements to align with celestial and spiritual beliefs. For instance, they specify methods to create geometric shapes such as squares and circles essential in ritualistic practices, reflecting an understanding of scaling and proportionality. This historical insight into the Sulba Sutras underscores the profound integration of geometry with spiritual and cultural practices, illustrating the practical implications of geometric transformations in ancient times.
Building on that foundation, we now move into the concept of geometric transformations. These transformations take basic shapes to new dimensions of understanding and application, allowing them to be scaled, mirrored, or adjusted in size while retaining their fundamental properties. This adaptability enhances the versatility of geometric shapes, making them applicable across various fields, from architecture and art to natural patterns and digital design.
In this post, we’ll explore three key types of transformations—scaling, similarity, and congruence. Each transformation holds unique value in Vedic science and Basic Geometry, illustrating how ancient practices employed these principles to create proportionate structures, intricate patterns, and harmonious designs. By mastering these transformations, we gain a deeper appreciation of geometry’s power to convey balance and order, effectively bridging the wisdom of Vedic science with modern applications.
Scaling
Definition
Scaling is a geometric transformation that involves altering the size of a shape while maintaining its proportions. This transformation is achieved by multiplying the dimensions of the shape by a constant, known as the “scale factor.”
Theoretical Explanation
When you scale a shape, every dimension of the shape is multiplied by the same constant—the scale factor. If the scale factor is greater than 1, the shape enlarges; if it’s less than 1, the shape reduces in size. Importantly, the shape’s proportions remain unchanged, ensuring that its geometric integrity is preserved.
Example for Scaling
Consider a rectangle with initial dimensions of 4 units by 3 units. If we apply a scale factor of 2, each dimension of the rectangle is multiplied by 2:
- The length is scaled from 4 units to 8 units (4 units × 2).
- The width is scaled from 3 units to 6 units (3 units × 2). The new dimensions of the rectangle are 8 units by 6 units, demonstrating how scaling affects the size of the shape while keeping its proportions consistent.
Applications in Vedic Science
In Vedic architecture, scaling is crucial for designing structures that need to reflect specific symbolic or ritualistic proportions. For example, scaling allows for the design of altars and temples to vary in size while maintaining specific proportional relationships prescribed in the Sulba Sutras.
Visual Example
The diagram would visually illustrate the rectangle before and after applying the scale factor, highlighting the proportional increase in size.
Exercise: Try this simple exercise to experience scaling:
- Draw a square with sides of 5 cm on graph paper.
- Choose a scaling factor of 1.5.
- Multiply each side length by the scaling factor (5 cm × 1.5 = 7.5 cm).
- Draw a new square with sides of 7.5 cm next to the original square, and observe how it retains its shape while increasing in size.
We can also try this exercise digitally, using design software with scaling tools. Experimenting with scaling gives hands-on experience with Vedic science’s approach to mastering geometric transformations, showcasing the balance and symmetry inherent in scaled shapes.
Similarity
Definition
Similarity is a geometric transformation that results in shapes maintaining the same angles and proportional side lengths but varying in overall size. This transformation ensures that shapes look identical in form but can differ in scale, which is crucial for applications that require maintaining visual harmony across different sizes.
Theoretical Explanation
When a shape undergoes a similarity transformation, all its dimensions are multiplied by a constant scale factor, similar to scaling, but the emphasis is on maintaining the shape’s angles and proportional dimensions. This means that the resulting shape, though different in size, will look the same and fit perfectly if superimposed over the original, aligning precisely at every angle and ratio.
Example for Similarity
Imagine a triangle with sides of 3 cm, 4 cm, and 5 cm. If we apply a similarity transformation with a scale factor of 2, each side of the triangle is scaled by 2:
- The side of 3 cm becomes 6 cm (3 cm × 2).
- The side of 4 cm becomes 8 cm (4 cm × 2).
- The side of 5 cm becomes 10 cm (5 cm × 2). The new triangle has sides of 6 cm, 8 cm, and 10 cm, respectively, maintaining the same shape and angles as the original but doubled in size.
Vedic Science Perspective
In Vedic art and architecture, similarity is used to create designs that resonate with cosmic order. By employing similar geometric patterns at various scales, these designs connect the microcosm (small scale) with the macrocosm (large scale), symbolizing universal harmony and continuity. This concept is evident in the intricate patterns found in temple architecture and sacred art, where similar motifs repeat across different scales to create a unified spiritual narrative.
Visual Example:
The diagram would visually display the original and transformed triangles, highlighting how the angles remain the same while the dimensions change proportionally.
Exercise: Try this exercise to better understand similarity:
- Start with a rectangle with dimensions 4 cm by 2 cm.
- Choose a similarity ratio of 0.5.
- Apply the ratio to each dimension (4 cm × 0.5 = 2 cm; 2 cm × 0.5 = 1 cm).
- Draw the new, smaller rectangle and compare it to the original, noting how it maintains the same proportions and angle orientation but at a reduced size.
This revised approach not only provides a detailed explanation of similarity but also connects it with practical and symbolic applications in Vedic science, making it more relatable and understandable for readers.
Congruence
Definition
Congruence in geometry refers to the exact matching of form and size between two shapes. Every dimension, angle, and property are identical, ensuring that congruent shapes can be perfectly overlaid on one another without any discrepancies.
Theoretical Explanation
Congruent shapes are essential in fields requiring high precision and uniformity, such as architecture and manufacturing. They maintain the integrity of designs and ensure that components fit seamlessly.
Visual Examples:
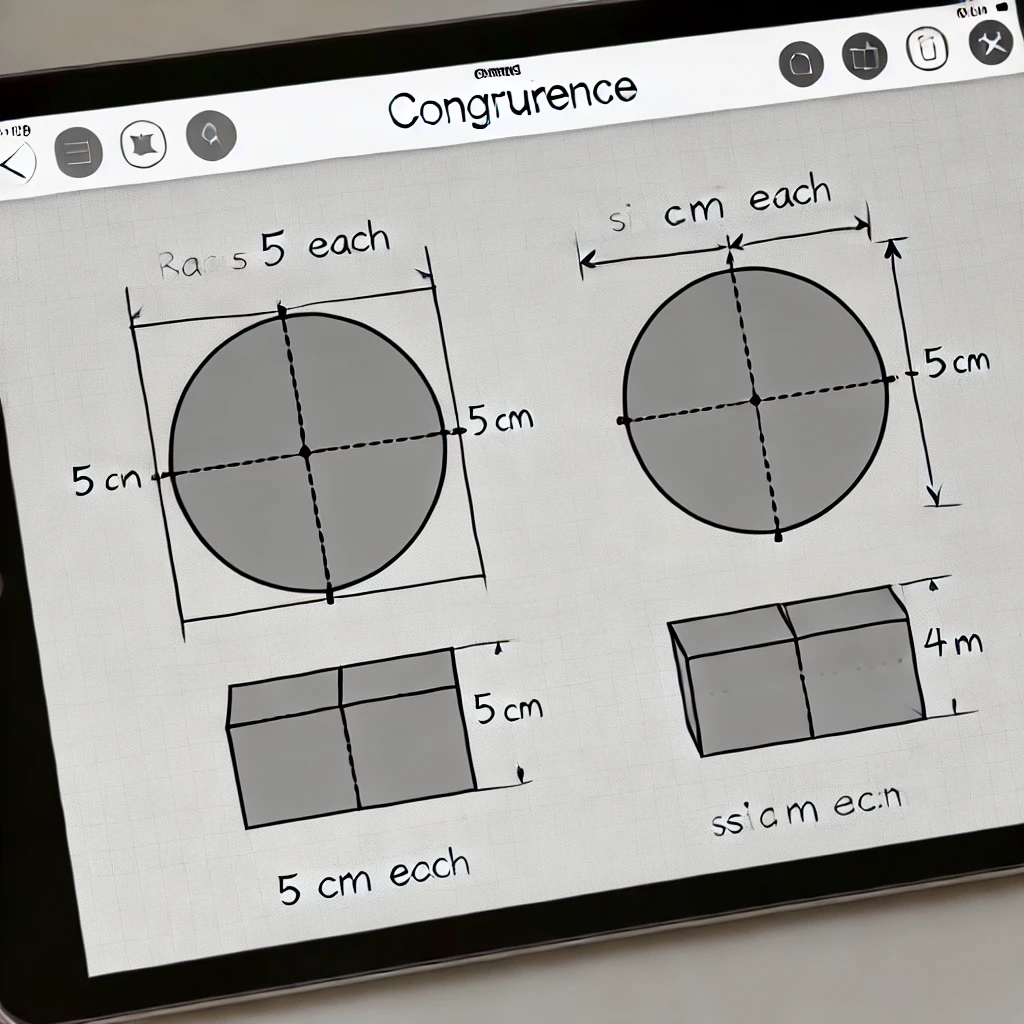
This image illustrates two congruent circles, each with a radius of 5 cm, demonstrating their identical dimensions. The clear labels and precise measurements highlight the exactitude necessary to establish congruence.
Practical Applications
Congruence is vital in architecture, where identical windows, doors, and other structural elements are necessary for aesthetic harmony and structural integrity. In manufacturing, it ensures that parts are interchangeable and assembly processes are efficient.
Exercise: To engage with the concept of congruence:
- Draw two circles on a piece of paper, each with a 5 cm radius.
- Encase each circle in a square, ensuring all sides of the squares are equal.
- Measure the sides of the squares and the radii of the circles to confirm their congruence.
This exercise, along with the visual examples provided in the images, helps reinforce the understanding of congruence by allowing you to apply and visualize this geometric principle effectively.
Practical Applications of Transformations
Geometric transformations like scaling, similarity, and congruence aren’t just mathematical concepts; they have practical applications in various fields, enhancing both functionality and aesthetics. From ancient Vedic practices to modern design, these transformations provide a foundation for creating balanced, proportionate, and visually engaging structures and patterns.
Applications in Architecture, Design, and Natural Symmetry:
Architecture
In Vedic-inspired temple architecture, congruent shapes maintain structural balance, while scaling and similarity allow for the creation of hierarchies and proportionate layouts. Larger main structures are often surrounded by similar, smaller elements, preserving harmony. This method of using geometric transformations in layout and design extends to modern architecture, where similar principles create flow and balance in urban planning and building design.
Design
Scaling and similarity are frequently applied in art and design to create patterns and motifs. In Vedic art, mandalas and yantras use similar and congruent shapes in repetitive arrangements, symbolizing cosmic order and unity. Modern graphic design echoes these techniques to create visual consistency and rhythm, making images and layouts more engaging and harmonious.
Natural Symmetry
Nature embodies geometric transformations, as seen in the scaling of patterns on seashells, the similarity of leaves on plants, and the congruence in crystal structures. Vedic science recognized these natural patterns, interpreting them as reflections of cosmic order. Today, the study of fractals and natural symmetry in fields like biology and environmental design reveals the same underlying principles that Vedic practitioners observed.
Relevance in Modern Fields
Modern fields like fractal geometry and computer graphics have continued to build on the principles of geometric transformations seen in Vedic science. Fractals—self-similar structures that maintain proportional patterns across different scales—reflect Vedic insights into natural and cosmic symmetry. These fractal designs are widely used in art, animations, and even ecological modeling, highlighting the enduring relevance of Vedic science and Basic Geometry in understanding and representing complex forms in the world around us.
By mastering transformations like scaling, similarity, and congruence, we tap into a timeless design language that spans ancient Vedic practices and contemporary applications, bridging science, art, and nature.
Reflections on Vedic Science helps Mastering Geometric Transformations
Vedic Science helps mastering geometric transformations such as scaling, similarity, and congruence. In this exploration, we delve into how these key transformations deepen our understanding of both Vedic science and Basic Geometry. These transformations enhance the functional and aesthetic applications of basic shapes and connect us to the rich symbolic meanings Vedic science attributes to balance, harmony, and cosmic order. By engaging with these transformations, we gain valuable insights into how ancient wisdom utilized geometry as a bridge between the physical and spiritual realms.
I encourage you to try these transformations with the shapes you constructed in the previous post. Experimenting with scaling, creating similar shapes, and ensuring congruence will help solidify these concepts and reveal the beauty of geometric relationships. In the next post, we’ll delve into the properties and measurements of these shapes, including how to calculate area and perimeter, further connecting geometry to practical applications and Vedic philosophy.
Call to Action
Have you tried scaling, similarity, or congruence with your shapes? Share your experiences or questions in the comments section—your insights can inspire others! And don’t forget to follow the blog for continued explorations into Vedic science and geometric principles as we journey through the fascinating world of ancient wisdom and modern mathematics.
Feature Image: Click here to view the image.
#VedicScience #GeometricTransformations #AncientGeometry #Mathematics #SacredGeometry
Related blogs
Vedic Science in Medicine- 1
Vedic Science Behind the Sun Temple of Konark
Vedic Cosmology And Rich Traditions of Vedic Science
Vedic science and its legacy
Science Hub of Ancient Times: Reviving Ancient Vedic Wisdom
Sun Temple of Konarak: A Challenges to Modern Science-II
Sun Temple Konark Architecture: A Challenges to Modern Science-I
Sun Temple: Vedic principles and Cosmic Connection
Konark Temple Marvels: Comparison With Peers-I
Konârak Temple Marvels: Comparison With Peers-II
Vedic Maths Illustrated: The Sundial at Konark Sun Temple
Vedic Mathematics: A Comparison with Conventional Methods
Agriculture in India: Comparing with Vedic Agriculture Principles
Yoga Day and Ashtanga Yoga In Hindu Philosophy
Vedic Science Principles of Maths and Astronomy
Vedic Science Principles of Maths and Astronomy
Vedic Science Principles of Life Science and Environment
Vedic Science Principles of Humanities and Farming
Vedic Science Principles of Philosophy and Other Sciences
Vedic Principles of Geometry and Measurement
Vedic science and Basic Geometry
References
https://ia800400.us.archive.org/2/items/VedicMathematics_201711/Vedic%20Mathematics.pdf
Leave a Reply